This page contains a selection of miscellaneous MATLAB tools, tircks and demos that I have written and am making available free for non-commercial use under the terms of the GNU General Public License (license.txt). I would be grateful if you would email me to let me know about any bugs you find or to give suggestions for improvements. If you find this software useful, please add a footnote in any resulting publication giving the URL of this page and let me know about it - the more times a peice of software is used successfully, the more reassured we can be that it is correct!

You may also be interested in my MATLAB Support Vector Machine (SVM) toolbox.

Software index:

• Sammon's nonlinear mapping
• Incomplete Cholesky factorisation
• Receiver Operating Characteristic (ROC) curve tools
• Optimisation tools

Tricks index:

• Hiding MEX files

Data index:

• Gunnar Raetsch's benchmark datasets

Demo index:

• Heteroscedastic kernel ridge regression
• Leave-one-out cross-validation of LS-SVMs

---

Sammon's Nonlinear Mapping

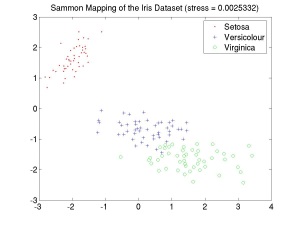
Sammon's nonlinear mapping algorithm [1] attempts to find a low-dimensional (normally 2- or 3-d) representation of a set of points distributed in a high dimensional pattern space, such that the Euclidean distance between points in the map are as similar as possible to the Euclidean distance between the corresponding points in the high-dimensional pattern space. For example, the image to the right shows a Sammon map of Fisher's famous Iris dataset [2], which records the widths and lengths of the petals and sepals of three varieties of Iris flowers (Setosa, Virginica and Versicolour). In this case the Sammon mapping produces a two-dimensional visualisation of the structure of a four-dimensional dataset. The value of the stress of the mapping in this case is very low (stress << 0.1), which indicates that the mapping gives a good idea of the underlying structure of the data.

The algorithm is implemented essentially as described in [1], except for the following:

• For ease of vectorisation, little advantage is taken of the symmetry of the pairwise distance matrices in the pattern and map spaces. This is fine for smallish datasets, but it may mean that the code is rather slow for very large datasets, where the extra computation out-weighs the benefits of vectorisation. As a result, the cost function minimised is essentially twice that given in [1], however the value of E returned by SAMMON is corrected to account for this, for ease of comparison.
• A simple step-halving approach is used, instead of Sammon's "Magic Factor", to avoid over-shooting the minima of the optimisation problem involved in forming the mapping. This was found to be rather faster in practice.

Downloads:

• m-file implementing Sammon's nonlinear mapping (sammon.m)
• minimal test harness using Fisher's Iris dataset (sammon_test.m)
• The original paper on the Sammon mapping [1], reproduced here with the kind permission of the IEEE (sammon.pdf)

References:

[1]	Sammon, John W. Jr., "A Nonlinear Mapping for Data Structure Analysis", IEEE Transactions on Computers, vol. C-18, no. 5, pp 401-409, May 1969.
[2]	Fisher, R. A. "The use of multiple measurements in taxonomic problems", Annual Eugenics, vol. 7, Part II, pp 179-188, 1936.

Back to the top

---

Incomplete Cholesky Factorisation

[R, p] = CHOLINCSP(X) finds a lower triangular Cholesky factor, R, of a symmetric positive semi-definite matrix, X, using the incomplete Cholesky factorisation with symmetric pivoting due to Fine and Scheinberg [1]. The second output argument, p, specifies a permutation of X, such that R*R' = X(p,p). If R has n columns, then the first n elements of p specify a set of linearly independent columns of X that provide a basis for the remaining columns of X (or at least a very close approximation). CHOLINCSP is useful to anyone interested in kernel learning methods, as it can be used to find a set of representers for constructing sparse kernel machines (i.e. the kernel expansion only includes terms corresponding to the training patterns represented by the columns of the Gram or kernel matrix used to form the Cholesky factor R, i.e. p(1:n)).

Downloads:

• m-file implementing incomplete Cholesky factorisation with symmetric pivoting (cholincsp.m)
• faster mex-file implementation using the BLAS library (cholincsp.m, cholincsp.c)
• minimal test harness / demonstration program (cholincsp_test.m)

Links:

• If your are interested in kernel learning methods, you may also want to check out Matthias Seeger's software page. He has implemented an incomplete Choelsky factorisation, where the kernel matrix is evaluated as part of the computation of the Cholesky factor. This should be faster as not all of the kernel matrix need be evaluated if a good sparse approximation can be found.

References:

[1]	Fine, S. and Scheinberg, K., "Efficient SVM training using low-rank kernel representations", Journal of Machine Learning Research, vol. 2, pp 243-264, December 2001.

Back to the top

---

Hiding MEX Files

hidemexfun.m provides a template for a simple trick allowing the use of MEX files to be hidden from the user, essentially by transparently compiling the MEX file the first time it is required. This is useful for distributing MATLAB packages containing MEX files in a reasonably platform independent manner. Basically, the first time the function is invoked, the MEX file will not have been compiled yet, so it will be m-file that is executed. The m-file then attempts to compile the MEX implementation and if sucessfull it recursively invokes itself. This time, the MEX file has been recompiled, so the compiled MEX function for that platform will now be present and MATLAB will invoke that version instead. The varargs mechanism is used to pass on all input and output arguments to the compiled MEX function. The rehash command is used to make sure that MATLAB notices that a compiled MEX version has appeared.

• This has been tested on the following platforms: Linux + MATLAB R14. If you find it works on a platform not listed here, please let me know and I'll add it to the list.
• The template relies on some features introduced in MATLAB R14, but it is fairly straight-forward to make a slightly less automated version that does not use these features.

Downloads:

• template m-file veneer for hiding MEX files (hidemexfun.m)
• example MEX file to be hidden (hidemexfun.c)
• (untested) template m-file veneer for hiding MEX methods (hidemexmethod.m)

Back to the top

---

Receiver Operating Characteristic (ROC) Curve Tools

An ROC (Receiver Operating Characteristic) curve is a plot of the true positive rate as a function of the false positive rate of a classifier system as the score defining the decision threshold is varied. This toolkit implements some of the basic methods for constructing and processing ROC curves discussed by Fawcett [1] and Provost and Fawcett [2]. The area under the ROC curve is a reasonable performance statistic for classifier systems assuming no knowledge of the true ratio of misclassification costs.

Downloads:

• m-file to compute ROC curve (roc.m)
• m-file to compute ROC convex hull (rocch.m)
• m-file to compute area under an ROC/ROCCH curve (auroc.m)
• demo/minimal test harness (rocdemo.m)

References:

[1]	Fawcett, T., "ROC graphs : Notes and practical considerations for researchers", Technical report, HP Laboratories, MS 1143, 1501 Page Mill Road, Palo Alto CA 94304, USA, April 2004 (pdf).
[2]	Provost, F. and Fawcett, T., "Robust classification for imprecise environments", Machine Learning, vol. 42, no. 3, pp. 203-231, 2001.

Back to the top

---

Gunnar Raetsch's Benchmark Datasets

This is a re-packaging of the thirteen benchark datasets from Gunnar Raetsch's web-site in order to conserve disk-space. These benchmark datasets have been widely used in model selection studies in kernel learning methods (e.g. [1-3]). Each benchmark is stored in a structure containing the unique input and target patterns, and a set of indices giving the 100 training and test splits (20 in the case of the image and splice datasets). For example, to reconstitute the forty-second realisation of the banana benchmark,

      >> load bencharks.mat banana
      >> x_train = banana.x(banana.train(42,:),:);
      >> t_train = banana.t(banana.train(42,:));
      >> x_test  = banana.x(banana.test(42,:),:);
      >> t_test  = banana.t(banana.test(42,:));

Downloads:

• For Matlab V7 (about 8Mb) (benchmarks.mat)
• For Matlab V6 (about 17Mb) (benchmarks_v6.mat)

References:

[1]	G. Raetsch, T. Onoda and K.-R. Muller, "Soft margins for AdaBoost", Machine Learning, vol. 43, no. 3, pp 287-320, March 2001.
[2]	S. Mika, G. Raetsch, J. Weston, B. Scholkopf and K.-R. Muller, "Fisher discriminant analysis with kernels", in Neural Networks for Signal Processing IX, pp 41-48, 1999.
[3]	Cawley, G. C. and Talbot, N. L. C., "Efficient leave-one-out cross-validation of kernel Fisher discriminant classifiers", Pattern Recognition, vol. 36, pp 2585-2592, 2003.

Back to the top

---

Heteroscedastic Kernel Ridge Regression Demo

Heteroscedastic Kernel Ridge Regression (HKRR) is a non-linear regression method for data exhibiting a heteroscedastic (input dependent) Gaussian noise process. The HKRR provides a model of both the conditional mean and the conditional variance of the target distribution. A more realistic estimate of conditional variance can be obtained using the leave-one-out cross-validation estimate of the conditional mean, giving the Leave-One-Out Heteroscedastic Kernel Ridge Regression (LOOHKRR) model (generally gives broader error bars). These methods are described in [1]. The demo given below applied conventional kernel ridge regression, HKRR and LOOHKRR methods to Silverman's motorcycle benchmark dataset.

Downloads:

• Heteroscedastic kernel ridge regression demo (hkrr_demo.m)

References:

[1]	G. C. Cawley, N. L. C. Talbot, R. J. Foxall, S. R. Dorling and D. P. Mandic, "Heteroscedastic Kernel Ridge Regression", Neurocomputing, vol. 57, pp 105-124, March 2004. (pdf, doi)

Back to the top

---

LS-SVM Leave-One-Out Cross-Validation Demo

Will appear here shortly...

Downloads:

• leave-one-out cross-validation demo (lssvm_demo.m)

References:

[1]	G. C. Cawley, "Leave-one-out cross-validation based model selection criteria for weighted LS-SVMs", Proceedings of the International Joint Conference on Neural Networks (IJCNN-2006), pages 1661-1668, Vancouver, BC, Canada, July 16-21 2006. (pdf)

Back to the top

---

Optimisation tools

This section will eventually contain a set of simple routines for non-linear optimisation problems. The first routine implements the Nelder-Mead simplex algorithm [1] for minimisation without the need for computing gradient information, providingmore or less the same functionality as the fminsearch routine from the MATLAB Optimisation Toolbox.

Downloads:

• Nelder-Mead simplex (simplex.m)

References:

[1]	J. A. Nelder and R. Mead, "A simplex method for function minimization", Computer Journal, vol. 7, pages 308-313, 1965.

Back to the top